Xác suất và đếm
May mắn. Trùng hợp. Ngẫu nhiên. Ko chắc chắn. Rủi ro. Nghi ngờ. May mắn. Cơ hội
Bạn đã đc nghe những từ này nhiều lần, nhưng theo cách mơ hồ, thông thường. Thật ko may, mặc cho sự phổ biến ở trong khoa học và đời sống, xác suất có thể cực kì phản trực giác (?!) Mục tiêu của cuốn sách là tạo ra 1 logical framework để định lượng sự ko chắc chắn và ngẫu nhiên theo cách có quy tắc. Chúng ta cũng củng cố trực giác, theo cả sự dự đoán có sẵn với lí giải logic và khi chúng ta ko may (phản trực giác).
- ubituity: ở khắp nơi (its ubiquity in science...)
- quantifying uncertainty: định lượng ...
1. Vì sao nghiên cứu xác suất?
Xác suất là logic của sự ko chắc chắn. XS hữu ích trong nhiều lĩnh vực, vì cung cấp công cụ để hiểu và giải thích các biến thể, tách tín hiệu khỏi nhiễu, lập mô hình hiện tượng phức tạp.
Vài ví dụ:
- Thống kê: Xs là nền và là ngôn ngữ của thống kế, cho phép nhiều phương pháp hiệu quả để sử dụng dữ liệu để học về thế giới.
- Vật lí: Vật lí lượng tử bao gồm xs ở mức nền tảng cơ bản của tự nhiên. Cơ học thống kê cũng là 1 nhánh khác của vật lí dựa trên xác suất
- Sinh học: Gen đc quyện vào nhau với xác suất, theo cả sự di truyền và lập mô hình đột biến ngẫu nhiên
- Khoa học máy tính: Các thuật toán ngẫu nhiên tạo ra các lựa chọn ngẫu nhiên khi chạy, và trong nhiều ứng dụng quan trọng chúng đơn giản hơn và hiệu quả hơn bởi các lựa chọn xác định. XS giúp nghiên cứu hiệu quả thuật toán, học máy và trí tuệ nhân tạo.
- Dự báo thời tiết: dự báo thời tiết đc tính và biểu thị bằng thuật ngữ xs
- Gambling (Liều): Nhiều nghiên cứu của xs đc dùng để trả lời các câu hỏi về sự liều và trò chơi cơ hội
- Tài chính: Rủi ro của sự dư thừa, xs là trung tâm của tài chính định lượng (quantiative finance). Mô hình giá cổ phiếu và việc xác định giá 'fair' cho ngành công nghiệp tài chính đc dựa trên xs.
- Khoa học chính trị
- Thuốc
- Cuộc sống
XS cung cấp các procedures cho việc giải quyết vấn đề 1 cách có quy tắc, nhưng cũng cung cấp các bẫy và nghịch lí. Các chiến lược để phòng tránh bẫy:
Các chiến lược
- Mô phỏng (Simulation)
- Biohazards: nghiên cứu các lỗi phổ biến giúp hiểu tốt hơn cái gì là hợp lí và ko hợp lí trong việc diễn giải xác suất.
- Sanity checks: Sau khi đã giải, ta thường thử giải vấn đề đó theo cách khác hoặc kiểm tra xem câu trả lời có đúng ở trường hợp đơn giản và cực đoan.
2. Không gian mẫu và thế giới sỏi
Framework toán học cho xác suất được xây dựng xoay quanh tập hợp. Tưởng tượng rằng khi 1 thí nghiệm đc thực hiện, kết quả ra 1 cái trong 1 tập hợp các kết quả có thể xảy ra. Trước khi thí nghiệm đc thực hiện, ta ko bik đc cái outcome (đầu ra) nào sẽ là kết quả; sau đó ,kết quả "kết tinh" thành 1 đầu ra thực sự.
Định nghĩa 1.2.1 ( ko gian mẫu và sự kiện)
(Sample space and event)
Không gian mẫu (The sample space) S cuả 1 thí nghiệm là tập hợp tất cả các đầu ra có thể của thí nghiệm. Một sự kiện A là 1 tập con của ko gian mẫu S, và ta nói A xuất hiện nếu đầu ra thực sự là A.
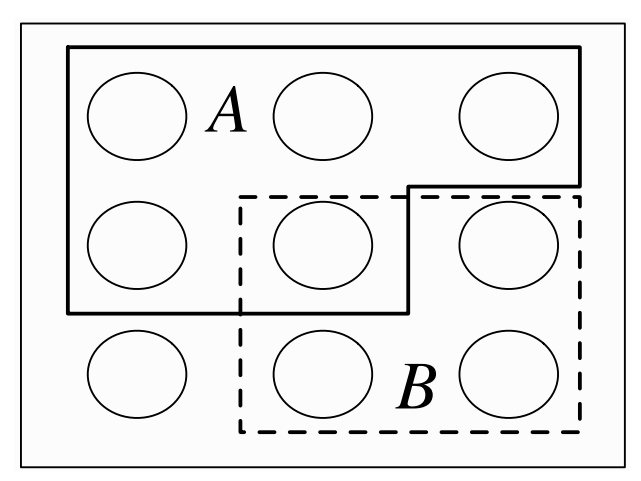
Hình 1.1. Một ko gian mẫu như là thế giới sỏi, với 2 sự kiện A và B đc làm nổi bật.
Một ko gian mẫu của 1 thí nghiệm có thể hữu hạn, vô hạn đếm đc hoặc vô hạn ko đếm dc. Khi một ko gian mẫu là hữu hạn, ta có thể hình dung nó như là 1 Pebble World (thế giới sỏi) như ở Hình 1.1. Mỗi viên sỏi đại diện 1 đầu ra, và 1 sự kiện là 1 tập các viên sỏi.
Thực hiện thí nghiệm tương đương với việc chọn ngẫu nhiên 1 viên sỏi.
- perform ... amounts to randomly selecting...
Nếu tất cả các viên sỏi có cùng khối lượng, tất cả các viên sỏi đều có khả năng đc chọn như nhau. (?!)
Lí thuyết tập hợp rất hữu ích trong xác suất, vì nó cung cấp 1 ngôn ngữ phong phú cho việc biểu thị và làm việc với sự kiện. Toán tử tập hợp, đặc biệt là hợp, giao, phần bù, giúp tạo ra các sự kiện mới dựa trên các sự kiện đã đc xác định. Các khái niệm này giúp ta mô tả 1 sự kiện nhiều hơn 1 cách; thường thì, 1 cách biểu thị 1 sự kiện dễ làm việc hơn cách biểu thị còn lại cho cùng 1 sự kiện.
Ví dụ, gọi S là 1 ko gian mẫu của 1 thí nghiệm và
Khi đó hợp () là sự kiện đc xuất hiện khi và chỉ khi ít nhất 1 cái của A và B xuất hiện; ...
Định luật De Morgan:
VD 1.2.2 ( tung xu)
1 đồng xu đc tung 10 lần. Viết ngửa là H(Head), sấp là T(Tail), 1 đầu ra có thể (viên sỏi) là HHHTHHTTHT, và 1 ko gian mẫu là tất cả các xâu (string) có độ dài 10 bao gồm các chữ H và T. Ta có thể mã hóa H là 1 và T là 0, để cho đầu ra là 1 dãy với và ko gian mẫu là tập tất cả các dãy như vậy. Bây giờ nhìn vào vài sự kiện:
- Lấy là sự kiện mà tung xu đầu tiên là ngửa. Tập hợp đó là : Đây là 1 tập con của ko gian mẫu, nên nó thực sự là 1 sự kiện. Nói xuất hiện tức là nói lượt tung xu đầu tiên là ngửa. Tương tự, gọi là sự kiện lần tung thứ là ngửa với .
- Lấy B là sự kiện mà có ít nhất 1 lượt tung xu là ngửa. Tâp hợp đó là:
- Lấy C là sự kiện mà tất cả các lượt tung đều là ngửa.
- Lấy D là sự kiện mà có ít nhất 2 lượt liên tiếp ngửa.